Singular Value Decomposition atau SVD dapat dirampatkan (diperumum) menjadi bentuk Generalized Singular Value Decomposition atau GSVD. Misalkan 
dan
merupakan matriks simetris definit positif yang masing-masing berukuran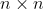 
dan 
, maka untuk setiap matriks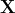 
berukuran 
yang memiliki pangkat 
dapat dinyatakan dengan:
di mana dari persamaan (1) diperoleh hubungan 
dan 
dengan 
merupakan nilai singular tertata yang diperoleh dari matriks 
(Greenacre 1984). Langkah-langkah perhitungan GSVD adalah:
1. Menghitung SVD dari
Cara memperoleh 
dan 
dengan menggunakan Penguraian Spektral atau SVD dari 
dan di mana 
dan 
. Sehingga 
dan
. Selanjutnya dihitung SVD dari misalkan hasilnya 
.
2. Mendefinisikan matriks 
Dengan memisalkan maka diperoleh:
3. Mendefinisikan matriks 
dan
Dengan mendefinisikan dan maka diproleh GSVD 
GSVD sering digunakan sebagai landasan dalam Analisis Korespondensi yang memeragakan baris dan kolom secara serempak dari tabel kontingensi dua arah, kemudian diperluas untuk tabel kontingensi banyak arah.
Semoga bermanfaat. . .
Daftar Pustaka:
Greenacre MJ. 1984. Theory
and Applications of Correspondence Analysis. London: Academic Press.
Siswadi. 2016. Ukuran Procrustes dalam suatu reduksi
dimensi. Orasi ilmiah guru besar IPB: Institut Pertanian Bogor.
Tidak ada komentar:
Posting Komentar