Complete Singular Value Decomposition dan Pendekatan matriks X

Pada artikel sebelumnya (klik sini) telah diuraikan tentang sejarah singkat dari Singular Value Decomposition atau SVD serta langkah-langkah dari penguraian matriks dengan menggunakan SVD. Nah, pada kesempatan ini, saya akan menguraikan tentang macam-macam dari SVD serta pendekatan suatu matriks terhadap matriks X.

Suatu matriks X berukuran n x p apabila diuraikan menjadi:

$_{n}\mathbf{X}_{p} = _{n}\mathbf{U}_{n}.\mathbf{L}. _{p}\mathbf{W}'_{p}$ , (1)

maka oleh Green & Carroll (1976) dan Greenacre (1984), persamaan (1) di atas disebut sebagai Complete Singular Value Decomposition atau CSVD dengan U dan W merupakan matriks ortogonal. dan L merupakan matriks yang disusun seperti seperti yang telah dijelaskan pada slide presentasi pada artikel sebelumnya (klik sini).

Sedangkan SVD itu sendiri didefinisikan sebagai:

$_{n}\mathbf{X}_{p} = _{n}\mathbf{U}_{r}.\mathbf{L}. _{r}\mathbf{W}'_{p}$ (2)

di mana pada persamaan (2), matriks U diperoleh dari matriks U pada persamaan (1) dengan dihilangkan $(n-r)$ kolom terakhirnya. W merupakan matriks yang diperoleh dari matriks W pada persamaan (1) denan menghilangkan $(p-r)$ kolom terakhirnya. L merupakan matriks diagonal yang anggota diagonal utamanya nilai-nilai eigen dari XX' atau X'X. Pada persamaan (2) diperoleh kondisi bahwa UU' = I dan W'W = I dengan setiap kolom pada U dan W merupakan vektor ortonormal (Greenacre 1984). Bentuk persamaan (2) akan ekuivalen dengan:

$_{n}\mathbf{X}_{p} = \sum_{i=1}^{r}\sqrt{\lambda_{i}}.\mathbf{u}_{i}.\mathbf{w}_{i}^{'}$ (3)

pada persamaan (3), jika nilai singular $\lambda _{s+1}, \lambda _{s+2}, ..., \lambda _{r}$ lebih kecil dibandingkan dengan $\lambda _{1}, \lambda _{2}, ..., \lambda _{s}$ maka menghilangkan $(r-s)$ suku terakhir dari persamaan (3) akan memberikan pendekatan yang baik dari matriks X dan memiliki pangkat $s$ yang tentunya lebih rendah daripada matriks X awal yang berpangkat $r$ . Hal tersebut berarti menghilangkan beberapa bagian yang diagnggap kurang penting secara sistematis. Teorema pendekatan pangkat rendah telah dibuktikan oleh Eckart & Young (1936) dengan hasil sebagai berikut:

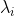Misalkan $\mathbf{A} = \sum_{i=1}^{s}\sqrt{\lambda _{i}}.\mathbf{u}_{i}.\mathbf{w}_{i}^{'}$ adalah matriks berukuran n x p dengan pangkat s yang berasal dari s nilai singular terbesar dan sama dengan nilai singular vektor-vektor dari X dengan $\mathbf{u} _{i}$ dan $\mathbf{w} _{i}$ merupakan vektor padanan dari nilai eigen $\lambda _{i}$ yang diperoleh dari XX' dan X'X secara berturut-turut, maka A merupakan matriks berpangkat s yang meminimumkan: $\left \| \mathbf{X}-\mathbf{A} \right \|=\left (\sum_{i=1}^{n}\sum_{j=1}^{p}\left ( x_{ij}-a_{ij} \right )^{2} \right )^{1/2}=\sqrt{trace\left \{ \left ( (\mathbf{X}-\mathbf{A})(\mathbf{X}-\mathbf{A})' \right ) \right \}}$

untuk setiap s < r. Hal tersebut sering digunakan dalam reduksi dimensi untuk mendapatkan pendekatan optimal dari matriks data antara lain melalui Principal Component Analysis atau Biplot Analysis.

Daftar Pustaka:

Eckart C, Young G. 1936. The approximation of one matrix by another of lower rank. Psychometrika, 3(1):211-218.

Green PE, Carroll JD. 1976. Mathematical Tools for Applied Multivariate Analysis. New York(US): Academic Press.

Greenacre MJ. 1984. Theory and Applications of Correspondence Analysis. London: Academic Press.